张荣斌，刘晨博，袁博秋，刘继斌，丁 浩 （国防科技大学 电子科学学院，长沙 ４１００７３）

摘要：随着电子信息设备数量激增与无线电频谱资源的深度开发，空间电磁环境日益复杂，大功率压制式干扰对雷 达、通信等设备的威胁显著增加。 现有射频前端干扰抑制技术存在电路复杂、自适应能力弱等问题，尤其难以应对非合作 未知干扰。 为此，本文提出一种基于双通道的射频前端自适应干扰抑制技术，在模拟域实现对干扰信号的相位自适应调 控，使两路干扰信号等幅反相对消，同时保护期望信号。 仿真结果显示，在 ３ ＧＨｚ 中心频点下，理想干扰抑制比达 ５３． ６０ ｄＢ， 期望信号损耗仅 １． ９３ ｄＢ；实验验证 ２ ＧＨｚ ～ ４ ＧＨｚ 频段内最大干扰抑制比超 ３６ ｄＢ，且在 ±１８０° 入射角度范围内保持稳 定。 该技术为解决射频前端大功率干扰抑制问题提供了新思路，兼具结构简化与自适应调控优势，对提升电子设备抗干 扰能力具有实际应用价值。

关键词：射频前端；干扰抑制；双通道；自适应

０ 引 言 

    电子信息设备数量的急剧增加和无线电频谱资源 的深度开发［１］引发了空间电磁信号密度的急剧攀升， 电磁环境日益复杂。 与此同时，随着高功率微波技术 的迅猛发展及应用［２］ ，雷达、通信等各类电子信息设 备自身受到干扰降级甚至损伤的风险也在逐渐增加。

    现有的干扰抑制技术按照干扰抑制处理的位置主 要分为两大类，分别为接收机数字后端干扰抑制技 术［３－４］和射频前端干扰抑制技术［５－６］ 。 数字后端干扰 抑制技术主要包括以数字信号处理为依托的抗干扰算 法、数字波束形成技术等，在面对强度较低的干扰信号 时，干扰抑制效果显著。 然而在面对大功率压制式干 扰时，由于前端链路的功率敏感器件饱和，基于数字处 理的干扰抑制技术将会失效［７］ 。 射频前端干扰抑制 技术在干扰进入放大链路前进行抑制，可有效避免前 端链路饱和，实现大功率的干扰抑制，其中较为经典的 技术方案包括Ｂｕｔｌｅｒ 矩阵电路［８－９］ 、基于正交 耦 合器［１０－１２］和多相滤波器［１３－１５］ 的射频耦合电路等。 但目 前上述技术的性能指标尚不能满足实际需求，仍面临 诸多困难和挑战，比如电路设计复杂、体积庞大、难以 根据电磁干扰信号变化实时调整抑制策略、自适应能 力较弱等。 并且现有的大部分射频前端干扰抑制技术 研究聚焦于系统的自干扰等已知干扰［１６－１７］ ，对于非合 作未知干扰的抑制技术研究仍处于探索和发展阶 段［１８］ 。 为进一步提升射频前端干扰抑制技术在高强 度干扰抑制、应对非合作未知干扰、结构简化与小型 化、自适应能力及灵活性等方面的综合性能，本文开展 了一种基于双通道的射频前端自适应干扰抑制技术的 研究。 自适应干扰抑制技术［１９－２１］ 的核心是实现干扰 信号的对消，同时保护期望信号不受影响，从而维持电 子信息设备的正常工作。 在自由空间中，信号的接收 具有方向性维度，即干扰信号和期望信号在来波方向 和距离上是可以区分的，具体体现到信号中则是幅度 和相位的差异，这为干扰抑制技术的研究提供了基础。 基于此，本文创新性地提出了一种自适应干扰对消结 构，通过利用干扰信号强度远超期望信号幅度的特点， 实现对干扰信号相位的自适应调控，并设计电路实现 在射频前端对未知干扰的自适应抑制。

１ 系统模型 

    本文提出了一种双通道自适应干扰对消结构，该 结构能够通过闭环反馈机制动态调节相位参数，在射 频端实现对干扰信号的抑制，其结构如图 １ 所示。

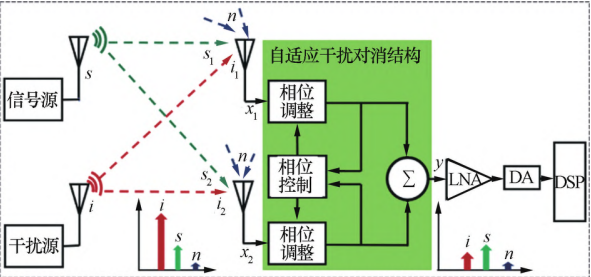
图 １ 双通道射频前端自适应干扰对消结构示意图 Ｆｉｇ． １ Ｓｃｈｅｍａｔｉｃ ｄｉａｇｒａｍ ｏｆ ａｄａｐｔｉｖｅ ｉｎｔｅｒｆｅｒｅｎｃｅ ｃａｎｃｅｌｌａｔｉｏｎ ｓｔｒｕｃｔｕｒｅ ｆｏｒ ｄｕａｌ⁃ｃｈａｎｎｅｌ ＲＦ ｆｒｏｎｔ⁃ｅｎｄ

    该双通道自适应干扰对消结构位于射频前端，介 于天线馈线端与低噪声放大器之间，由相位调整模块、 相位控制模块和信号合成模块组成。 信号分别从两个 接收通道进入两个相位调整模块，经过相位调整之后 耦合出一部分进入相位控制模块，相位控制模块根据 输入的耦合信号，控制其中一路的相位调整模块进行 相位调节，使两路通道内的干扰信号达到等幅反相状 态，再通过合成两路等幅反相的干扰信号，实现对干扰信号的抑制。

    双通道自适应干扰对消电路对干扰信号的抑制过 程如图 ２ 所示。 输入信号经过移相器移相后先进行合 成，将合成后的信号使用耦合器耦合出一部分用于检 波。 由于干扰强度远超期望信号，因此检波结果主要 由功合器输出中干扰信号的幅度决定。 检波输出控制 其中一路压控移相器移相，形成负反馈环路，最终使两 个通道内的干扰信号相位相反，从而通过功合器合成 实现反向对消。 检波控制电路由低噪声放大器、检波 器、模拟数字转换器（ＡＤ）、数字模拟转换器（ＤＡ） 和 ＦＰＧＡ 组成，借鉴自适应信号处理中的功率倒置算法， 通过使输出信号功率最小这一约束准则，对其中一个 通道的输入信号进行移相，从而使两个通道内的干扰 信号相位差接近 １８０°。

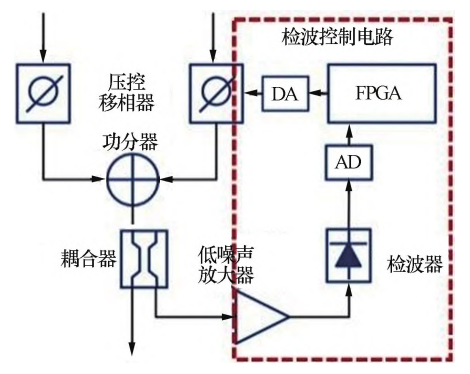
图 ２ 自适应干扰对消电路结构图 Ｆｉｇ． ２ Ｓｔｒｕｃｔｕｒａｌ ｄｉａｇｒａｍ ｏｆ ａｄａｐｔｉｖｅ ｉｎｔｅｒｆｅｒｅｎｃｅ ｃａｎｃｅｌｌａｔｉｏｎ ｃｉｒｃｕｉｔ

２ 干扰抑制数学过程 

２． １ 干扰对消数学模型 

    下面以单频连续波干扰为例阐述干扰对消数学模 型。 假设噪声为加性高斯白噪声，期望信号为单频连 续波信号，期望信号 ｓ（ｔ）和单频连续波干扰信号 ｉ（ｔ） 分别为

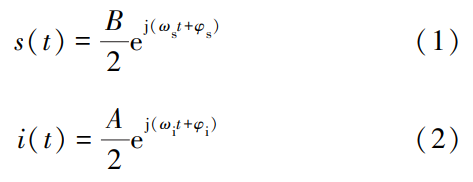
式中：ωｓ 和 ωｉ 分别为期望和干扰信号的信号频率；φｓ 和 φｉ 分别为期望和干扰信号的初始相位。 由于信号 到达两个天线单元存在路径差，会产生不同的相位延 迟，设期望信号和干扰信号的相位延迟分别为 ϕｓ 和 ϕｉ，则到达两个天线单元的期望信号 ｓ１（ ｔ）和 ｓ２（ ｔ）分 别表示为

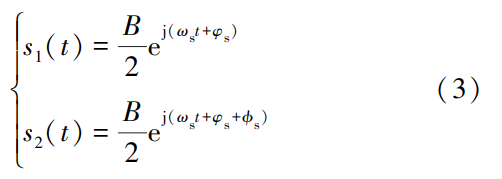
    单频连续波干扰信号 ｉ １（ｔ）和 ｉ ２（ｔ）表示为

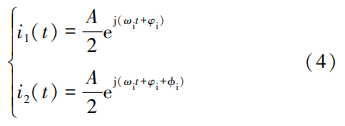
    噪声信号为加性高斯白噪声信号，其概率密度函 数为

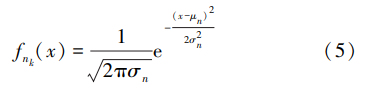
式中：μｎ ＝ ０；σ ２ ｎ 为方差。 两个天线单元接收到的噪声 信号分别为 ｎ１（ｔ）和 ｎ２（ｔ），相互独立。

    两个天线单元的接收信号 ｘ１（ｔ）和 ｘ２（ｔ）表示为

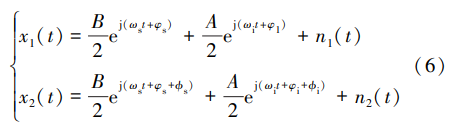
    由于假设接收天线为两个完全相同的二元天线单 元，所以接收信号 ｘ１（ｔ）和 ｘ２（ｔ）中的干扰信号分量 ｉ １（ｔ） 和 ｉ ２（ｔ）的幅度相等。 要使结构中两个通道内的干扰 信号等幅反相，只需要对其相位进行调整。 假设对两 个通道的相位调整分别为 Ψ１ 和 Ψ２ ，则合成输出信号 ｙ（ｔ）为

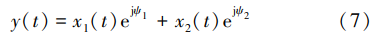
式中：合成输出信号 ｙ（ｔ）中的干扰信号分量为

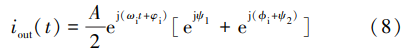
理想情况下，使 ｅ ｊψ１＋ｅ ｊ（ϕｉ ＋ψ２ ） ＝ ０ 时，合成输出信号 中的干扰信号分量 ｉ ｏｕｔ（ ｔ）被完全对消，此时相位需要 满足的条件为

式（９）表明，当两个接收通道的相位调整 Ψ１ 和 Ψ２ 的差值与干扰信号在两个通道间的相位差 ϕｉ 之和 为 π 的奇数倍时，也就是将两个通道内干扰信号调整 为反相时，合成输出信号中的干扰分量被完全对消，理 想情况下干扰信号的抑制比为正无穷大（＋∞ ）。

    合成输出信号 ｙ（ｔ）中的期望信号分量为

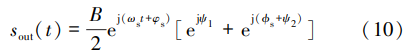
    理想情况下，期望信号要满足同相叠加条件时，合成输出信号中的期望信号分量 ｓｏｕｔ（ｔ）最大，此时相位 需要满足的条件为

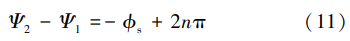
    当两个通道的相位调整满足式（１１）时，合成输出 信号中期望信号分量 Ｓｏｕｔ（ｔ）的功率增益最大，理想情 况下，期望信号的最大增强比为 ３ ｄＢ。

    而当相位满足式（９）时，即干扰信号分量被完全 对消时，将其带入式（１０），得出合成输出信号中的期 望信号分量 Ｓｓｏｕｔ（ｔ）为

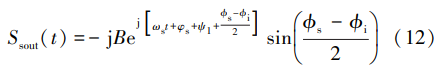
    干扰信号分量完全对消条件下，由式（１２） 可知， 期望信号分量 Ｓｓｏｕｔ（ｔ）的幅度与相位差 ϕｓ －ϕｉ 相关，即 合成输出后的期望信号增益，与两路干扰信号的相位 差和两路期望信号的相位差的差值相关。 当 ϕｓ ＝ ϕｉ 时，干扰信号被对消的同时，期望信号也被完全对消； 当 ϕｉ －ϕｓ ＝ π，干扰信号被对消的同时，期望信号被同 相叠加，增益达到最大。 ϕｓ 和 ϕｉ 与入射角度 θｓ 和 θｉ 以及接收信号的波长 λｓ 和 λｉ 有关，也就是说，要符合 条件 ϕｓ≠ϕｉ，需要干扰信号入射角 θｓ 和期望信号入 射角 θｉ 不一致，或者干扰信号频率与期望信号频率 不一致。

２． ２ 自适应相位调整数学模型 

    在实际的干扰对消电路中，一般无法达到理想的 对消条件，即两路信号不能实现完全的等幅反向，导致 合成输出信号中的干扰分量不能完全对消。 下面对双 通道自适应干扰对消结构的相位调整机制进行分析， 讨论实际电路的调整误差对干扰抑制比的影响。 双通 道自适应干扰对消结构的数学模型如图 ３ 所示。

图 ３ 自适应干扰对消结构的数学模型 Ｆｉｇ． ３ Ｍａｔｈｅｍａｔｉｃａｌ ｍｏｄｅｌ ｏｆ ｔｈｅ ａｄａｐｔｉｖｅ ｉｎｔｅｒｆｅｒｅｎｃｅ ｃａｎｃｅｌｌａｔｉｏｎ ｓｔｒｕｃｔｕｒｅ

    对于压控移相器，假设在电压 ＶＰ 范围内的移相角 度为 ３６０°，那么压控移相器的移相灵敏度 α（°／ Ｖ）可 以定义为

    对于检波器，其输出电压 Ｖｏｕｔ 与检波功率 Ｐｄｅｔｅｃｔ 成一次函数关系，可以表示为

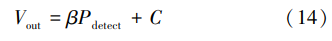
式中：β（Ｖ／ ｄＢｍ）表示检波输出电压随检波信号功率 变化曲线的斜率；Ｃ 为常数。

    对于 ＦＰＧＡ，假设其位数为 ｎ，则其最多具有 Ｎ＝ ２ ｎ 个状态值；假设 ＤＡ 的电压输出区间为［Ｖｍｉｎ ，Ｖｍａｘ］，则 通过 ＤＡ 输出的最小电压步进值 Ｖｄ 为

    ＦＰＧＡ 通过 ＤＡ 输出 Ｎ 个离散电压 Ｖ２ｋ，移相器进 行 Ｎ 次移相，每次的相移角度 θｋ 为 αＶ２ｋ，采集每个 Ｖ２ｋ 对应的检波电压 Ｖ１ｋ，对比后找到使 Ｖ１ｋ 最小的 Ｖ２ｃｔｒ１ ， 此时干扰抑制效果达到最佳。

    由于干扰信号、期望信号和噪声信号相互独立，电 路的自适应相位调整过程不会改变噪声信号的特性， 且噪声信号不会影响相位调整结果，所以为了简化分 析过程，暂时忽略噪声信号的影响，只关注干扰信号和 期望信号。 为了进一步简化分析过程，假设干扰信号 和期望信号均为初始相位为 ０ 的正弦信号，两个通道 接收到的信号分别为

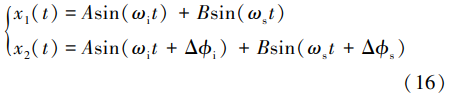
式中：Ａ、ωｉ、Δϕｉ 分别为干扰信号的幅度、频率、在两个 通道间的相位差；Ｂ、ωｓ、Δϕｓ 分别为期望信号的幅度、 频率、在两个通道间的相位差，且满足 Ａ＞＞Ｂ、Δϕｉ≠Δϕｓ 的条件。

    两路信号第 ｋ 次经过压控移相器移相后变为

式中：θｋ ＝ αＶ２ｋ 为移相器第 ｋ 次对信号的相移量，功合 器合成的输出信号 ｙｋ（ｔ）为

式中：分别为第 ｋ 次移相合成后的干扰 信号分量和期望信号分量，其表达式分别为

ｙｋ（ｔ）经过耦合器和低噪放处理后到达检波器时为

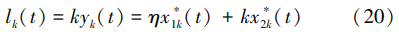
式中：η 由耦合器的耦合度和低噪声放大器的倍数决 定，检波信号 ｌ ｋ（ｔ）功率为

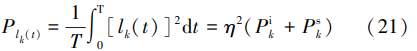
式中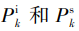：分别为第 ｋ 次的干扰信号功率和期望 信号功率，其表达式分别为

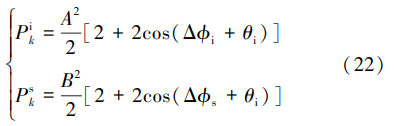
检波信号 ｌ ｋ（ｔ）经过检波器后输出的检波电压 Ｖ１ｋ 为

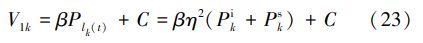
在 Ａ＞＞Ｂ 的条件下，检波器第 ｋ 次检测到的信号功 率为 Ｐｄｅｔｅｃｔｋ≈η ２Ｐ ｉ ｋ，当 Ｐｄｅｔｅｃｔ 最小时，即 Ｐｄｅｔｅｃｔ≈η ２Ｐ ｉ ｋ→ ０，此时 θｋ→－Δϕｉ －π，即两个通道内的干扰信号趋近于 反相，且由于 Δϕｉ≠Δϕｓ，期望信号得以保留。 此时，最 小 Ｐｄｅｔｅｃｔｋ 对应的最佳控制电压 Ｖ２ｃｔｒ１ 为

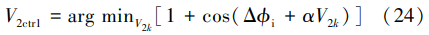
从数学角度看，自适应相位调整的过程本质是在 有限相位调整范围 Ｎ 内求解式（２４）最优解的问题。 

３ 电路模型仿真与实验 

３． １ 电路仿真

    使用 Ｍａｔｌａｂ 对自适应干扰对消结构进行数学模型 仿真，假设二元天线阵列的天线间距 ｄ 为 λ／ ２，λ 按照中 心频点 ｆ ０ 为 ３ ＧＨｚ 进行计算，信号的初始相位为 ０。

    输入信号的参数包括：干扰信号功率 Ａ、频率 ωｉ、入 射角度 θｉ；期望信号功率 Ｂ、频率 ωｓ、入射角度 θｓ，其具 体数值设置如表 １ 所示。

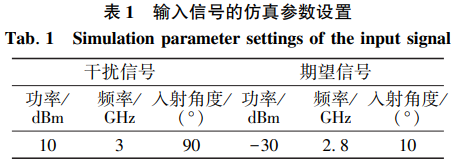
    仿真后得到干扰抑制前后输入信号的频谱对比 图，如图 ４ 所示。 从仿真结果可以看出，双通道射频前 端自适应干扰对消结构按照表 １ 所示参数建模后对干 扰信号具有 ５３． ６０ ｄＢ 的理想干扰抑制效果，与此同 时，期望信号仅有 １． ９３ ｄＢ 的损耗。

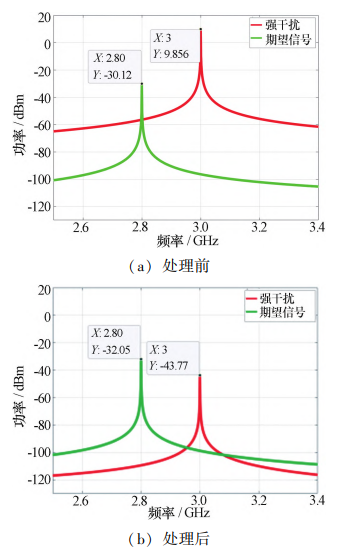
图 ４ Ｎ 为 ２５６ 时自适应干扰对消结构处理前后信号的频谱对比图 Ｆｉｇ． ４ Ｓｐｅｃｔｒｕｍ ｃｏｍｐａｒｉｓｏｎ ｄｉａｇｒａｍ ｏｆ ｓｉｇｎａｌｓ ｂｅｆｏｒｅ ａｎｄ ａｆｔｅｒ ｐｒｏｃｅｓｓｉｎｇ ｂｙ ｔｈｅ ａｄａｐｔｉｖｅ ｉｎｔｅｒｆｅｒｅｎｃｅ ｃａｎｃｅｌｌａｔｉｏｎ ｓｔｒｕｃｔｕｒｅ（Ｎ＝２５６）

    设定两个天线单元接收信号幅度完全一致的前提 下，移相误差是影响电路模型干扰抑制效果的主要因 素。 电路的移相误差由电路的移相精度决定，电路的 移相精度越高，可能产生的移相误差越小。 电路的移 相精度为 ＦＰＧＡ 输出电压的步进 Ｖｄ（Ｖ／ °）与压控移相 器的相移灵敏度 α（°／ Ｖ）的乘积，由式（１３）和式（１５） 可知，电路的移相精度 θｄ 为

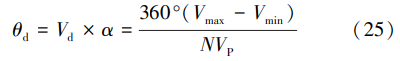
式中：ＦＰＧＡ 输出用于控制压控移相器的最小电压 Ｖｍｉｎ 、最大电压 Ｖｍａｘ 与压控移相器的移相范围 ＶＰ 保持 一致，而 ＶＰ 由压控移相器所使用的变容二极管决定。 所以在理想电路状态下，电路的移相精度 θｄ 由 ＦＰＧＡ 输出电压的状态数 Ｎ 决定。

    将 ＦＰＧＡ 输出电压的状态数 Ｎ 设置为 １２８，其余 仿真参数按照表 １ 设置，仿真得到 Ｎ 为 １２８ 时干扰抑 制前后输入信号的频谱对比图，如图 ５ 所示。

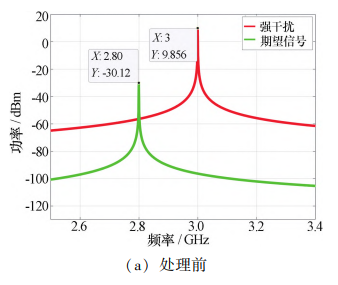
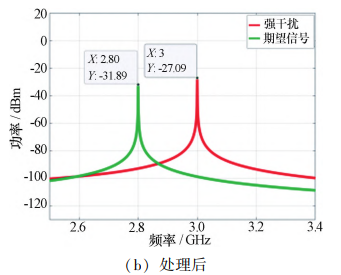
图 ５ Ｎ 为 １２８ 时自适应干扰对消处理前后信号频谱对比图 Ｆｉｇ． ５ Ｓｐｅｃｔｒｕｍ ｃｏｍｐａｒｉｓｏｎ ｄｉａｇｒａｍ ｏｆ ｓｉｇｎａｌｓ ｂｅｆｏｒｅ ａｎｄ ａｆｔｅｒ ａｄａｐｔｉｖｅ ｉｎｔｅｒｆｅｒｅｎｃｅ ｃａｎｃｅｌｌａｔｉｏｎ ｐｒｏｃｅｓｓｉｎｇ （Ｎ＝ １２８）

    当 Ｎ 为 １２８ 时，理想电路模型对干扰信号的干扰 抑制比为 ３６． ９５ ｄＢ，对期望信号的损耗为 １． ７７ ｄＢ。 与 Ｎ 为 ２５６ 时对比，理想干扰抑制比下降了 １６． ６５ ｄＢ，期 望信号损耗下降了 ０． １６ ｄＢ。 说明当减小 ＦＰＧＡ 输出 电压的状态数为 Ｎ 时，电路的干扰抑制效果下降，但 对期望信号的损耗也相应降低。

    将 ＦＰＧＡ 输出电压的状态数 Ｎ 设置为 ５１２，仿真 得到 Ｎ 为 ５１２ 时干扰抑制前后输入信号的频谱对比 图，如图 ６ 所示。

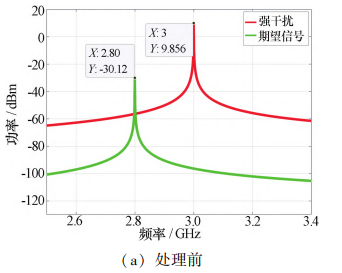
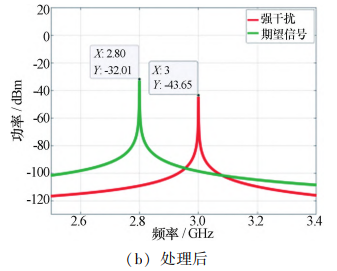
图 ６ Ｎ 为 ５１２ 时自适应干扰对消处理前后信号频谱对比图 Ｆｉｇ． ６ Ｓｐｅｃｔｒｕｍ ｃｏｍｐａｒｉｓｏｎ ｄｉａｇｒａｍ ｏｆ ｓｉｇｎａｌｓ ｂｅｆｏｒｅ ａｎｄ ａｆｔｅｒ ａｄａｐｔｉｖｅ ｉｎｔｅｒｆｅｒｅｎｃｅ ｃａｎｃｅｌｌａｔｉｏｎ ｐｒｏｃｅｓｓｉｎｇ （Ｎ＝ ５１２）

    当 Ｎ 为 ５１２ 时，理想电路模型对干扰信号的干扰 抑制比为 ５３． ５１ ｄＢ，对期望信号的损耗为 １． ８９ ｄＢ。 与 Ｎ 为 ２５６ 时相比，干扰抑制比在误差范围内保持一 致，期望信号损耗也大致保持。 说明当 ＦＰＧＡ 输出电 压的状态数 Ｎ 增加到 ５１２ 时，状态数 Ｎ 对电路的干扰 抑制效果的影响减弱。 即使用状态数 Ｎ 为 ２５６ 的 ＦＰＧＡ 可大致满足电路的移相误差设计要求。

    为了评估双通道射频前端自适应干扰对消结构可 抑制干扰信号的入射角度范围，基于入射角度的空间 对称性，在正半轴空间范围内改变干扰信号的入射角 度 θｉ，其余参数按照表 １ 设置进行模型仿真，得到干扰 抑制效果随干扰入射角度的变化曲线，如图 ７（ａ）所示。

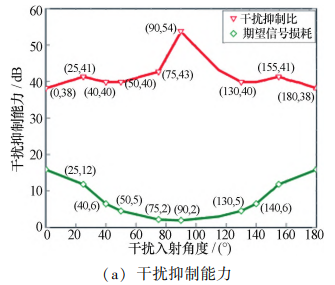
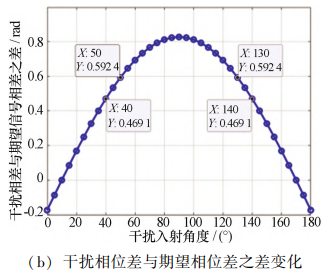
图 ７ 干扰抑制能力随干扰入射角度变化曲线 Ｆｉｇ． ７ Ｃｕｒｖｅ ｏｆ ｉｎｔｅｒｆｅｒｅｎｃｅ ｓｕｐｐｒｅｓｓｉｏｎ ｃａｐａｂｉｌｉｔｙ ｖａｒｙｉｎｇ ｗｉｔｈ ｉｎｔｅｒｆｅｒｅｎｃｅ ｉｎｃｉｄｅｎｔ ａｎｇｌｅ

    从图 ７（ａ）可知，在干扰信号（３ ＧＨｚ）、期望信号 （２． ８ ＧＨｚ，入射角为 １０°）场景下，当干扰入射角在 ０° ～ １８０°范围内连续变化时，理想电路模型始终保持 ３８ ｄＢ 以上的干扰抑制比。 由于空间入射角度的对称性，该 结构在－１８０° ～ ０°的负半轴空间也同样具有相同的干 扰抑制特性。

    期望信号损耗主要与干扰信号在两个通道间的相位 差 Δϕｉ 与期望信号在两个通道的相位差 Δϕｓ 之差 Δϕｉ － Δϕｓ 相关。 为了进一步量化期望信号损耗受 Δϕｉ －Δϕｓ 的 影响程度，仿真了 Δϕｉ －Δϕｓ 随干扰入射角度 θｉ 的变化曲 线，如图 ７（ｂ）所示。 可以看出，图 ７（ａ）中的两条曲线的 变化趋势 Δϕｉ －Δϕｓ 与随 θｉ 的变化曲线一致。 且电路的 干扰抑制比和期望信号损耗均受 Δϕｉ －Δϕｓ 影响。 当 Δϕｉ －Δϕｓ 的弧度值大于 ０． ４６９ 时，即 Δϕｉ －Δϕｓ 大于 ２６． ８７°时干扰抑制效果较好。 说明双通道射频前端自 适应干扰对消结构控制期望信号损耗在 ６ ｄＢ 以内的 条件下，期望信号与干扰信号相位差至少要相差 ２６． ８７°。 

３． ２ 实验测试

    在微波暗室中进行空间辐照式实验，其实验原理和实验场景如图 ８ 所示。

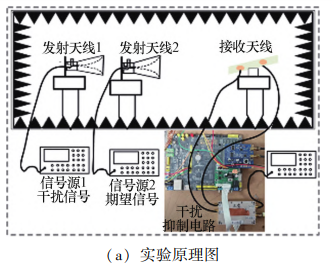
图 ８ 辐照式实验原理及场景图 Ｆｉｇ． ８ Ｓｃｈｅｍａｔｉｃ ｄｉａｇｒａｍ ｏｆ ｉｒｒａｄｉａｔｉｏｎ ｅｘｐｅｒｉｍｅｎｔ ｐｒｉｎｃｉｐｌｅ ａｎｄ ｓｃｅｎａｒｉｏ

    采用两个喇叭天线分别连接两个信号源发射信 号，用于模拟干扰信号和期望信号，二元阵列天线作为 接收天线。 测试时，先对链路进行校准，将接收天线的 两个输出端口的一端接匹配负载，另一端接入频谱仪， 分别读取干扰抑制前的干扰信号功率和期望信号功 率。 校准后，将接收天线的两个输出端口连接双通道 射频前端自适应干扰对消电路，并将电路的射频输出 端接入频谱仪。 根据抑制前后的信号功率，可以计算 得到干扰抑制电路的干扰抑制比和期望信号损耗。

    设置期望信号的频率为２． ９０ ＧＨｚ，发射功率为 －３０ ｄＢｍ；干扰信号的频率为 ２． ９５ ＧＨｚ，发射功率为 ０ ｄＢｍ，发射信号均为单频连续波信号。 其干扰抑制 效果如图 ９ 所示。 从测试结果可以看出，干扰抑制比 为 ３６． ７０ ｄＢ，期望信号损耗为－３． ３３ ｄＢ。

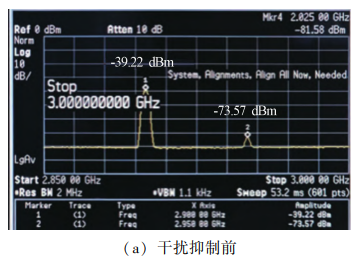
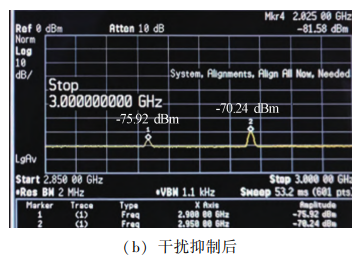
图 ９ 干扰抑制前后频谱图 Ｆｉｇ． ９ Ｓｐｅｃｔｒｕｍ ｄｉａｇｒａｍ ｂｅｆｏｒｅ ａｎｄ ａｆｔｅｒ ｉｎｔｅｒｆｅｒｅｎｃｅ ｓｕｐｐｒｅｓｓｉｏｎ

    进一步测试 ２ ＧＨｚ ～ ４ ＧＨｚ 频率范围内的干扰抑 制性能，依次改变干扰信号与期望信号的频率，进行单 频连续波干扰抑制实验，实验结果如图 １０ 所示。

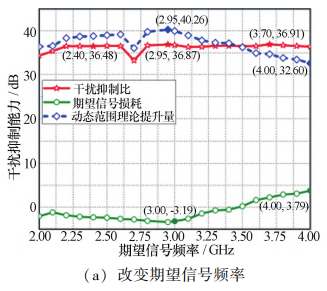
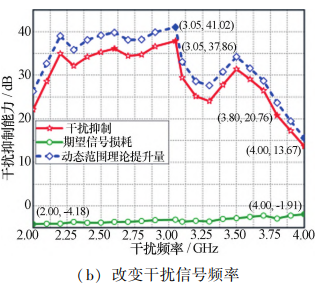
图 １０ 不同频率信号下干扰对消电路的干扰抑制效果 Ｆｉｇ． １０ Ｉｎｔｅｒｆｅｒｅｎｃｅ ｓｕｐｐｒｅｓｓｉｏｎ ｅｆｆｅｃｔ ｏｆ ｔｈｅ ｉｎｔｅｒｆｅｒｅｎｃｅ ｃａｎｃｅｌｌａｔｉｏｎ ｃｉｒｃｕｉｔ ｕｎｄｅｒ ｄｉｆｆｅｒｅｎｔ ｆｒｅｑｕｅｎｃｙ ｓｉｇｎａｌｓ

    由图 １０ 可知，当干扰信号频率固定为 ２． ９０ ＧＨｚ 时，设置不同频率的期望信号，电路的干扰抑制比保持 在 ３６． ５０ ｄＢ 附近，对期望信号的损耗最小为－３． １９ ｄＢ， 最大为 ３． ７９ ｄＢ，动态范围理论提升量最高为 ４０． ２６ ｄＢ。 当期望信号频率固定为 ３ ＧＨｚ 时，设置不同频率的干 扰信号，电路的干扰抑制比最高为 ３７． ８６ ｄＢ，最小为 １３． ６７ ｄＢ，对期望信号的损耗最小为－４． １８ ｄＢ，最大为 １． ９１ ｄＢ，动态范围理论提升量最高为 ４１． ０２ ｄＢ。

    上述实验结果说明，本文设计的双通道射频前端 自适应干扰对消电路能够自适应实现大功率干扰信号 的抑制功能，电路在 ２． ０ ＧＨｚ ～３． ８ ＧＨｚ 频率范围内干扰抑制比均大于 ２０ ｄＢ，其干扰抑制比最高可达 ３７． ８６ ｄＢ。

    与公开发表的文献相比，文献［１０－１１］实现干扰 抑制需要已知干扰信号的先验信息，自适应能力较弱， 且干扰抑制能力也较弱。 本文和文献［１２］ 可实现对 未知干扰约为 ４０ ｄＢ 的自适应抑制，但本文在信号通 道数量方面具有一定的优势，电路结构更易实现。 并 且本文提出的电路位于 ＬＮＡ 之前，在对抗大功率干扰 信号时可以实现高强度干扰抑制，能避免出现大功率 干扰信号使功率敏感器件（如 ＬＮＡ）饱和失真的情况， 可以有效提升接收机系统的工作动态范围。

４ 结束语

    本文针对射频前端在面对大功率压制式干扰时， 接收系统前端链路的功率敏感器件易饱和的情况，在 现有的抗干扰手段失效或者适应性不佳的前提下，提 出了一种双通道射频前端自适应干扰对消结构。 该结 构利用二元阵列天线接收两路信号，通过对两路信号 的相位调整，实现两通道中干扰信号的对消。

    仿真和实验结果表明，本文提出的结构能有效抑 制干扰信号，且在干扰入射角度±１８０°范围内均保持 良好的干扰抑制效果。 同时利用 ＦＰＧＡ 实现的自适应 调控功能，使得该对消电路在 ２ ＧＨｚ～４ ＧＨｚ 频率范围 内都能有较好的干扰对消性能。

张荣斌　男，１９９６ 年生，硕士生。主要研究方向：射频微波技术。

刘晨博　男，２０００ 年生，硕士生。主要研究方向：电磁防护技术。

袁博秋　女，１９９９ 年生，硕士生。主要研究方向：微波元器件和电磁防护。

刘继斌　男，１９７４ 年生，博士，教授。主要研究方向：微波电路、天线及电磁防护。

丁　浩（通信作者）　男，１９９０ 年生，博士，副教授。主要研究方向：射频通道强电磁压制与毁伤综合防护。